Lorentz' dev blog

Writing a neural network from scratch in C (part 2)

This post is part 2 in a series.

• Part 1: Linear regression
• Part 2: Neural networks

In this part we will take a look at how perceptrons and neural networks imitate the human brain.

Writing a neural network from scratch in C (part 1)

This is the first part of my notes on trying to learn machine learning and implementing a simple neural network from scratch in C. The code is intentionally very raw - we don’t even have a function matrix multiplication, I think this makes the details in the algorithms and math stand out more.

The source code can be found here: https://github.com/loldot/nn

Linear regression

An linear function is a function with a single variable whose graph looks like a straight line. We can generalize the function as having a weight \(w\) and a bias \(b\). Changing the weight will change the slope of the line, and changing the bias will change where the line intersects the y-axis. You might remember this equation from high school:

This simple equation can have predictive power if the data fits a line. For example assume we own a small ice cream shop and start measuring the temperature at midday and count our number of ice creams sold. After a few days of measurements, we have the following data:

Packing for a trip

Say you’re going somewhere you’ve never been before. Like my hometown, Bergen in Norway. And let’s say you go there during the winter.

You read about Roald Amundsen. He’s a Norwegian. Bet he’s got some great insights on packing for the Norwegian winter. Sure, he went to Antarctica, but his ideas surely carry over to your trip to Norway - it’s practically the arctic. With some items added to your packing list and some good survival tips for the arctic climate, you decide to do some more research.

You come across the Apollo 11 mission to the moon. What a fantastic expedition. NASA sure knows how to handle the most extreme conditions. You’re guaranteed to learn something that could be applied to your expedition to Bergen. Winter there is of course not as hostile as the environment on the moon, but it never hurts to be on the safe side. Maybe you should get a space suit? No - that would be silly. They’re really cool though. Maybe you should pick one up and experiment with it. You never know when that knowledge might come in handy.

You pack your bags. Prepared for whatever the harsh, Norwegian nature can bring, you go to the airport.

When you finally get to Bergen, you’re too warm and move slowly because your backpack is 50kg, and to be honest you didn’t have time to do the required workout beforehand, so you’re really exhausted. Worst of all: No one thinks you look smart and well prepared in your polar expedition gear. You look like a dumb cruise tourist.

How I use git

I use git religiously, even for tiny projects that I will probably be the only one to work on. In my first job, we used team foundation server from Microsoft. It was not a very pleasant experience. TFS is a centralized source control and project management system, and all I can remember from using it is:

• Files locked by a person on vacation
• Merge conflicts being so tedious to resolve that you constantly wanted to go implement the feature from scratch.

So you can imagine that I was not very enthusiastic when a new coworker got his will and was allowed to change the source control system to git - a feature that had just been introduced to TFS-server.

I’ll be the first to admit that I fucked up more than a few branches in the early days of using git. But unlike with TFS, there was always a way to recover. I just had to ask the aforementioned coworker, and he could turn the cli into a time machine. That was a long time ago now, and at this point I am a devout convert.

PEXT Tables

Introduction

Chess engines need to be incredibly fast. A common way to achieve fast generation of moves from a chess position, is to pre-calculate all the moves available for each piece type, from each square on the board, but disregarding pins and checks, this is usually called pseudo-legal moves. For pawns, knights and the king, this is fairly straightforward. Rooks, bishops and queens are a different matter; the moves available from each square is also dependent on where the other pieces are placed on the board.

Update: How to use multiple Microsoft accounts without going insane

I have meant to give an update on the previous post for a long while, but never got aroundt to it. I no longer use Chrome for many reasons, most of which are not relevant here, but one of them is that Firefox official addon for multi-account containers is so much better than the Chrome experience. In stead of having to manage multiple windows, you can use different profiles for each tab. The tabs are marked with colors which makes it easy to see when you are in a different context. You can right click to open a link in a different container. Right clicking the new tab button also allows you to choose which container you want to work in. I’ll also be the first to admit that the UX around multiple Microsoft accounts have improved alot since the original post, but I still like the Firefox extension. I use this for lots of other things now as well, i.e. logging in as different test users etc. Never switching back to Chrome again.

Cleaning out the bike shed

Ozan Yarcı showed an example of an anti-pattern on twitter and it sparked a lot of engagement.

TryHackMe writeup - Umbrella

Umbrella is a medium machine on TryHackMe with the description: “Breach Umbrella Corp’s time-tracking server by exploiting misconfigurations around containerisation.”

The case of the disappearing digits

BSidesBos CTF writeup - Web

I only solved two web challenges in this CTF: skid and Yet Another Micro-story Library. All web challenges had a pretty low number of solves.

Hacktivitycon writeup - Template Shack

Template Shack was a challenge worth 150 points in the 2020 Hacktivitycon CTF. The template shack appears to be some sort of online shop for bootsrap themes. The site seems to be mostly static and placeholder code. The only thing of note in the source code for the page is a comment that hints at some administration panel that is under construction.

TryHackMe writeup - Overpass

Here’s how I rooted the room overpass on tryhackme.com. All in all, the room was pretty easy, but I actually spent a lot of time figuring it out because I was overthinking.

How to use multiple Microsoft accounts without going insane

Update: I no longer use Chrome. See https://lorentzvedeler.com/2025/02/17/Update-Multiple-Microsoft-Accounts/ instead.

For the last couple of weeks I have had sort of an identity crisis. Working as a consultant, I have too many credentials for o365/azure/azure AD; being signed in to the right account at the right time has become impossible. Luckily there is a feature in chrome that will cure you of any virtual schizophrenia. If you click your name at the top of the title bar, you’ll find a menu with a choice to manage people.

This will take you to a management screen that lets you add people you can switch between.

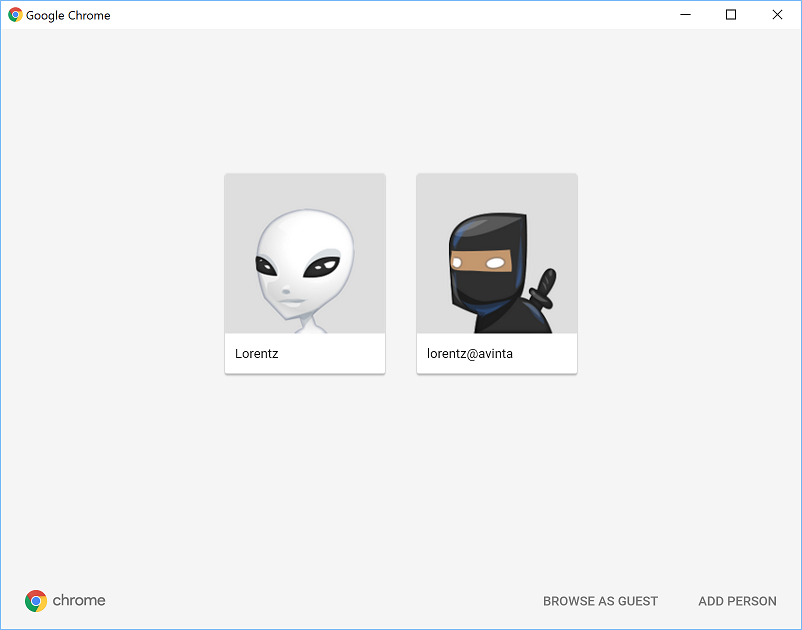
Now you’ll be able to easily switch between your personalities. Each personality has its own private data, so your sessions will be completely separate. They also have a separate window with a custom icon so that it’s easy to distinguish them from each other. Awesome!

Maintain the same version no. across multiple .net assemblies

If you want several projects to always have the same version number, this is a pretty neat trick:

1. Remove AssemblyVerison and AssemblyFileVersion from existing AssemblyInfo.cs files

2. Add a CommonAssemblyInfo.cs file to one of the projects containing just:

    using System.Reflection;
   
    [assembly: AssemblyVersion("2.3.1.0")]
    [assembly: AssemblyFileVersion("2.3.1.0")]
   

3. In the other projects add existing item choose the CommonAssemblyInfo.cs, but remember to add it as a link (click on the arrow on the add button)

Keyed Collection

This week I found a cool .net-class in the System.Collections.ObjectModel namespace; the class KeyedCollection<TKey,TItem>.

It provides a collection that can be indexed by a property. If your item-class has a natural key, all you have to do is derive from the abstract KeyedCollection-class and implement the GetKeyForItem method. It behaves pretty much like a mix between a dictionary and a list. Lookups are indexed by a key you can specify, which in turn is used as the key for an internal dictionary, and so are faster than searching a regular list.

It is documented further here.

public class SchoolClass : KeyedCollection<uint, Student>
{
    protected override uint GetKeyForItem(Student newStudent) => newStudent.Number;
}

Euler Problem 92

Here’s my solution to Euler problem 92. The code is pretty simple, it tries to shortcut the sequence by storing every number in a chain along with the number that recurs.

class Euler92:
    def __init__(self):
        self.knownSeq = {}

    def ChainNumber(self,n):
        currentSeq = []
        while not n in [1,89]:
            currentSeq.append(n)
            if(n in self.knownSeq):
                n = self.knownSeq[n]
            else:
                n = SquareDigits(n)
        for x in currentSeq:
            self.knownSeq[x] = n
        return n

    def Solve(self, n):
        return len([x for x in range(2,n) if self.ChainNumber(x) == 89])
        
def SquareDigits(n):
        return sum(map(lambda x: int(x)**2, str(n)))

Euler Problem 59

This is my solution to Euler problem 59 in python. It is pretty straight forward and relies on the heuristics of the problem. Initially it filters out every key that will only produce printable characters for all its corresponding positions in the encrypted text. It then proceeds to combine these keys and check for actual, common English words in the text.

from math import ceil
import string

def test():
    asciis = open('cipher1.txt', 'r').read()
    encCodes = [int(s) for s in asciis.split(',')]

    asciiSum = 0
    
    pKeys = plausibleKeys(encCodes, 3)
    for k0 in pKeys[0]:
        for k1 in pKeys[1]:
            for k2 in pKeys[2]:
                text = "".join(applyKey([k0,k1,k2], encCodes))
                if(properStringProbability(text)):
                    print(text)
                    asciiSum = sum([ord(c) for c in text])
    return asciiSum

def plausibleKeys(encCodes, keyLen):
    pKeys = {
        0: [x for x in range(255)],
        1: [y for y in range(255)],
        2: [z for z in range(255)]
        }

    for i, c in enumerate(encCodes):
        for k in pKeys[i % keyLen]:
            if chr(c ^ k) not in string.printable:
                pKeys[i % keyLen].remove(k)
    return pKeys

def properStringProbability(string):
    cnt = 0
    for word in ["the", "and", "have", "that", "you"]:
        cnt += string.count(word)        
    return cnt > 5


def applyKey(key, asciiText):
    return [chr(x ^ int(y)) for (x,y) in zip(key * int(ceil(len(asciiText) / 3)),asciiText)]